Příprava na přijímací zkoušky SŠ
TEST č. 13 – 16 týdnů do přijímaček
MATEMATIKA
1. Změřte vzdálenost mezi středy kružnice opsané a vepsané trojúhelníku ABC, je-li dáno : c = 6 cm, α = 75º , β = 45º.
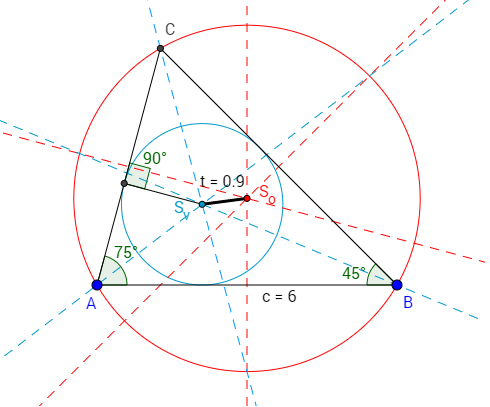
Slovní popis konstrukce:
- Narýsujeme úsečku AB v délce 6 cm
- U vrcholu A narýsujeme úhel 75º
- U vrcholu B narýsujeme úhel 45º
- Na průsečíku ramen označíme bod C
- Všem stranám trojúhelníku narýsujeme osy souměrnosti: do kružítka vezmeme větší vzdálenost než polovina úsečky, naznačíme oblouky nad i pod úsečkou, spojením dvou vzniklých průsečíků, narýsujeme osu souměrnosti.
- Průsečík os souměrnosti stran je středem kružnice opsané, poloměr je vzdálenost od středu ke kterémukoliv vrcholu trojúhelníku.
- Všem úhlům u vrcholů trojúhelniku narýsujeme osy souměrnosti, průsečík os souměrnosti je středem kružnice vepsané.
- Abychom získali poloměr kružnice vepsané, musíme ke středu kružnice vepsané narýsovat kolmici ke kterékoliv straně trojúhelníku.
- Poloměr kružnice vepsané je vzdálenost od středu k patě kolmice.
- Vzdálenost mezi středy kružnice vepsané a opsané je přibližně 1 cm.
2. Obchodník si vzal na osm měsíců úvěr 100 000 Kč při roční úrokové míře 11%. Kolik korun bude muset obchodník bance vrátit?
Roční úrok je 11 %,
měsíční úrok činí 11/12 %,
úrok za 8 měsíců je 8 . 11/12 %.
| 100 %
|
100 000
|
| 7,33 %
|
x
|
$\frac{x}{100000}=\frac{7,33}{100}$
$x=\frac{100000.7,33}{100}$
$x=7330$
Za osm měsíců zaplatí obchodník 7 330 Kč.
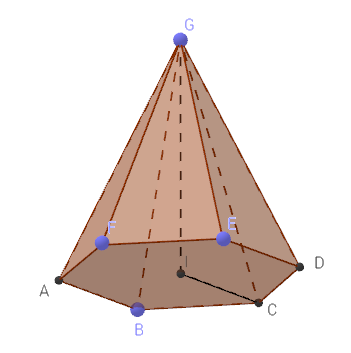
3. Podstavou pravidelného jehlanu je šestiúhelník, kterému můžeme opsat kružnici o poloměru 1 metr. Boční hrana měří 2 metry.
Vypočtěte :
a) objem jehlanu
b) povrch jehlanu
Objem jehlanu
- Obsah podstavy
Podstavu tvoří šest rovnostranných trojúhelníků, jejichž strana měří 1 m.
$S_{p} = 6 \times \frac {a . v_{a}}{2}$
Výšku trojúhelníku podstavy vypočteme pomocí Pythagorovy věty:
$v_{a}^{2}=a^{2}-\frac{a}{2}^{2}$
$v_{a}^{2}=1^{2}-0,5^{2}$
$v_{a}^{2}=0,75$
$v_{a}=0,87\;m$
$S_{p} = 6 \times \frac {1.0,87}{2}$
$S_{p} = 6 \times 0,44$
$S_{p} = 2,64\;m^{2}$
$V = S_{p} \times v$
Výšku jehlanu vypočteme pomocí Pythagorovy věty:
$v^{2}=2^{2}-1^{2}$
$v^{2}=3$
$v=1,73\;m$
$V = \frac{S_{p} \times v}{3}$
$V = \frac{2,64 \times 1,73}{3}$
$V = \frac{4,57}{3}$
$V = 1,52\;m^{3}$
Povrch jehlanu
Povrch jehlanu tvoří podstava a šest totožných trojúhelníků.
Obsah podstavy = $S_{p} = 2,64\;m^{2}$
Obsah pláště
Pomocí Pythagorovy věty vypočteme výšku trojúhelníku, který tvoří plášť
$v_{p}^{2}=h^{2}-\frac{a}{2}^{2}$
$v_{p}^{2}=2^{2}-0,5^{2}$
$v_{p}^{2}=3,75$
$v_{p}=1,94\;m$
$S_{pl} = 6 \times \frac {1.1,94}{2}$
$S_{pl} = 6 \times 0,97$
$S_{pl} = 5,82\;m^{2}$
$S = S_{p} + S_{pl}$
$S = 2,64 + 5,82$
$S = 8,46\;m^{2}$
Český jazyk
1. Škrtni slova, která nejsou příbuzná se slovem CESTA.
stanice – cestička – cestář – cestující – cestovní – cestovatel – cetka
2. Následující slova použij vždy ve dvou různých větách či slovních spojeních tak, aby šlo pokaždé o jiný slovní druh. Slova ponechej v zadaném tvaru.
VEČER
1. příslovce: Přijdeme až večer.
2. podstatné jméno: Byl krásný letní večer.
MÍSTO
1. podstatné jméno: Každý ve třídě má své místo.
2. předložka: Běž tam míto mě.
PILA
1. podstatné jméno: Pila byla velmi ostrá.
2. sloveso: Žíznivá fena pila dlouho.
3. Uvedenou větu napište správně:
Kdyby mně poslouchal, nemuseli bysme sebou brát o jeden kufr navíc.
Kdyby mě poslouchal, nemuseli bychom s sebou brát o jeden kufr navíc.
4. Určete mluvnické číslo u podtržených slov: Do krmítka jsme nasypali zrní. Otec natíral dveře.
krmítka: jednotné
zrní: jednotné
dveře: množné
5. Slovo psaní může být konkrétní i abstraktní. Rozhodněte na základě textu:
a) psaní od kamaráda: konkrétní
b) psaní odpovědi: abstraktní