Souřadnice v prostoru

Pokud pracujeme v rovině předpokládáme, že je v ní zvolena nějaká kartézská soustava souřadnic 0xy, a pokud pracujeme v prostoru, je v něm zvolena nějaká kartézská soustava souřadnic 0xyz.

Trojice číselných os x, y, z v prostoru je taková, že:

1. každé dvě z nich jsou navzájem kolmé,
2. všechny procházejí jedním bodem O,
3. bod O odpovídá na všech osách číslu 0.

Postup zakreslení bodu A [3;5;4] v prostoru:

1. na ose x nalezneme bod vzdálený 3 jednotky od počátku a vedeme jím přímku rovnoběžnou s osou y,
2. na ose y nalezneme bod vzdálený 5 jednotek od počátku a vedeme jím přímku rovnoběžnou s osou x,
3. vzniklým průsečíkem vedeme přímku rovnoběžnou s osou z,
4. na ose z nalezneme bod vzdálený 4 jednotky od počátku a vedeme jím přímku rovnoběžnou s úsečkou, která spojuje počátek s průsečíkem přímek rovnoběžných s x a y (nejdříve postupujeme, jak jsme zvyklí v rovině [x;y] a poté musíme vzniklý bod posunout podle osy z; pořadí bodů nesmíme zaměnit!).

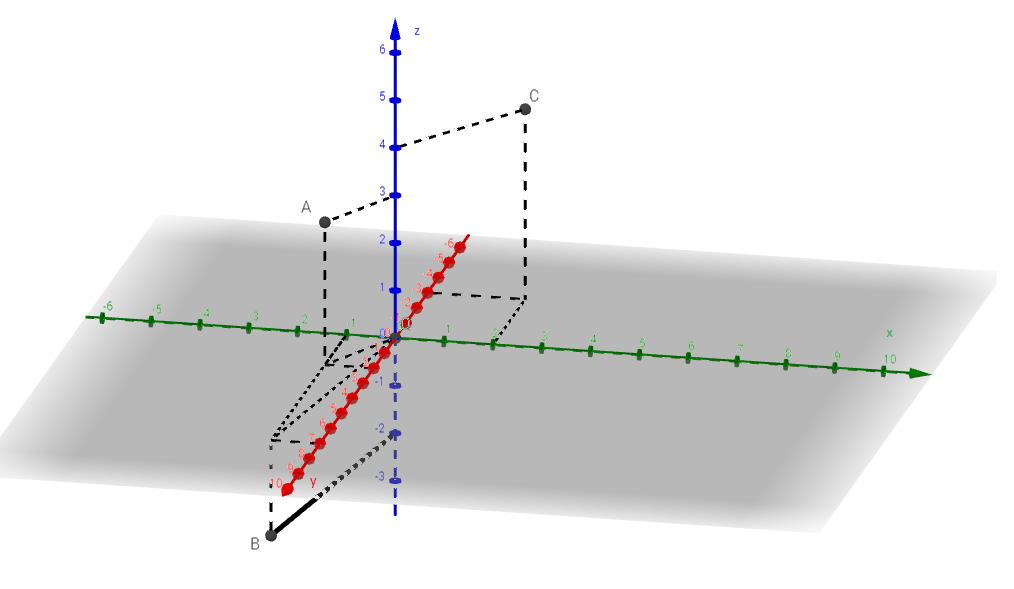
V kartézské soustavě souřadnic Oxyz ve volném rovnoběžném promítání zakreslete body A[-1;2;3], B[-1;7;-2], C[2;-3;4].

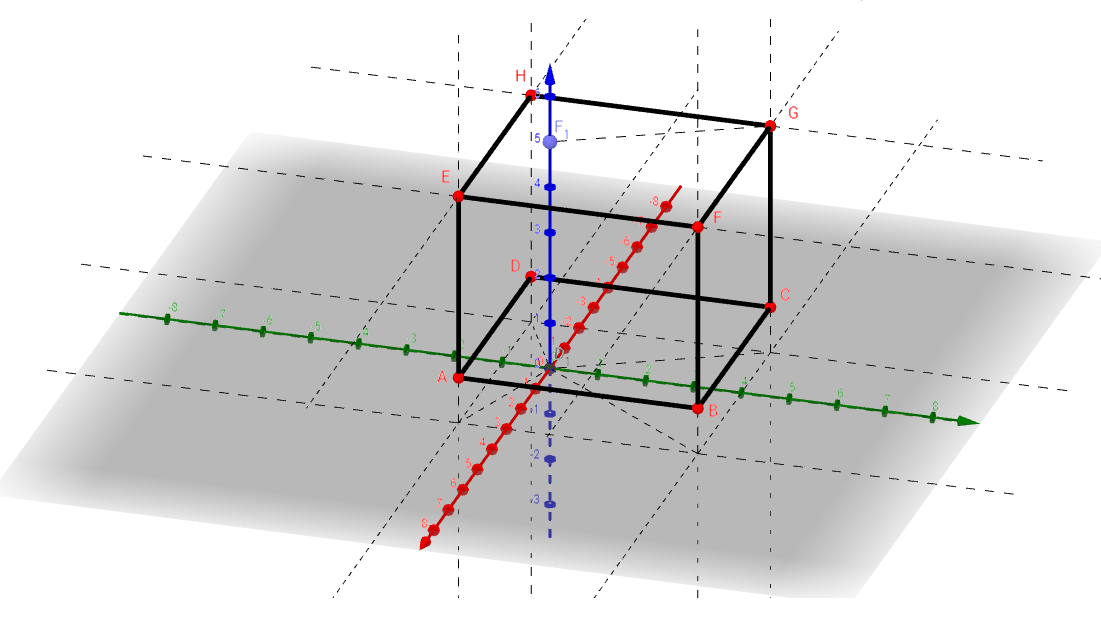
Ve volném rovnoběžném promítání zakreslete kartézskou soustavu souřadnic Oxyz. V ní zakreslete kvádr ABCDEFGH, pro který platí:

A[-1;3;1], B[4;3;1], C[?;-2;1], E[?;?;5]. Určete všechny souřadnice všech vrcholů kvádru.