1. Vypočítej objem a povrch pravidelného čtyřbokého jehlanu, který má délku hrany podstavy 45 cm a výšku 7 cm.
$a=45\;cm$
$v=7\;cm$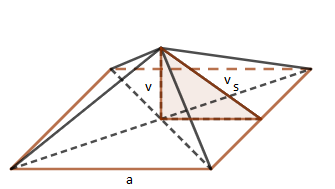
| $Výpočet\; stěnové\; výšky$
|
$Objem$
|
$Povrch$
|
|
$v_{s}^{2}=v^{2}+(\frac{a}{2})^{2}$ $v_{s}^{2}=7^{2}+22,5^{2}$ $v_{s}=23,56\;cm$ |
$V=\frac{a^{2}\times v}{3}$
$V=\frac{45^{2}\times 7}{3}$ $V=4724\;cm^{3}$ |
$S=S_{p}+S_{pl}$
$S=a^{2}+4\frac{av_{s}}{2}$ $S=45^{2}+2\times 45\times 23,56$ $S=4149\;cm^{2}$ |
2. Jehlan s obdélníkovou podstavou má rozměry a = 6 cm, b = 8 cm. Boční hrany jsou shodné a jejich délka h = 12,5 cm. Vypočítej povrch jehlanu.
$a=6\;cm$
$b=8\;cm$
$h=12,5\;cm$
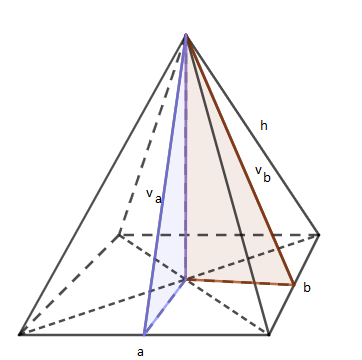
| $Výpočet\; stěnové\; výšky\;v_{a}$
|
$Výpočet\; stěnové\; výšky\;v_{b}$
|
$Povrch$
|
|
$v_{a}^{2}=h^{2}-(\frac{a}{2})^{2}$ $v_{a}^{2}=12,5^{2}-3^{2}$ $v_{a}^{2}=12,13\;cm$ |
$v_{b}^{2}=h^{2}-(\frac{b}{2})^{2}$
$v_{b}^{2}=12,5^{2}-4^{2}$ $v_{b}^{2}=11,84\;cm$ |
$S=S_{p}+S_{pl}$
$S=(a\times b)+2\frac{a\times v_{a}}{2}+2\frac{b\times v_{b}}{2}$ $S=6\times 8+6\times 12,13+8\times 11,84$ $S=215,5\;cm^{2}$ |
3. Krychle má délku hrany 12 dm, je do ní vepsaný jehlan s vrcholem ve středu horní stěny kostky. Vypočítej objem a povrch tohoto jehlanu.
$a=12\;dm$
$v=12\;dm$

| $Výpočet\; stěnové\; výšky$
|
$Objem$
|
$Povrch$
|
|
$v_{a}^{2}=v^{2}+(\frac{a}{2})^{2}$ $v_{a}^{2}=12^{2}+6^{2}$ $v_{a}=13,42\;dm$ |
$V=\frac{a^{2}\times v}{3}$
$V=\frac{12^{2}\times 12}{3}$ $V=576\;dm^{3}$ |
$S=S_{p}+S_{pl}$
$S=a^{2}+4\frac{av_{s}}{2}$ $S=12^{2}+2\times 12\times 13,42$ $S=466\;dm^{2}$ |
4. Kolik litrů vzduchu je pod střechou věže, která má tvar pravidelného šestibokého jehlanu s hranou podstavy délky 3,6 m a výškou 2,5 m, Předpokládejme, že krovy střechy zabírají asi 7% objemu prostoru pod střechou?
$a=3,6\;m$
$v=2,5\;m$
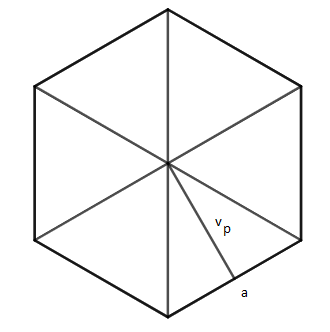
| $Výpočet\; v_{p}$
|
$Obsah\;podstavy$
|
$Objem$
|
|
$v_{p}^{2}=a^{2}-(\frac{a}{2})^{2}$ $v_{p}^{2}=3,6^{2}-1,8^{2}$ $v_{p}=3,12\;m$ |
$S_{p}=6\times \frac{a\times v_{p}}{2}$
$S_{p}=3\times a\times v_{p}$ $S_{p}=3\times 3,6 \times 3,12$ $S_{p}=33,7 \;m^{2}$ |
$V=\frac{S_{p} \times v}{3}$
$V=\frac{33,7 \times 2,5}{3}$ $V=28,08\;m^{3}$ |
| $zaokrouhlený\; výsledek$
$100\; \text{%}= 28,08 \; m^{3}=28080 \;l $ $93\;\text{%} =26114 \; l $ |
$výsledek\; bez\; zaokrouhlení$
$\large V=0,93\times \frac{3\times a\times \sqrt{a^{2}-(\frac{a}{2})^{2}} \times v}{3}$ $\large V=0,93\times\frac{3\times 3,6\times \sqrt{3,6^{2}-(\frac{3,6}{2})^{2}} \times 2,5}{3}$ $\large V=26095\;l$ |
5. Rotační kužel a rotační válec mají stejný objem 180 cm3 a stejnou výšku v = 15 cm. Které z těchto dvou těles má větší povrch?
| Válec
|
Kužel
|
| $V=180\;cm^{3}$
|
$V=180\;cm^{3}$
|
| $v=15\;cm$
|
$v=15\;cm$
|
| $Výpočet\; poloměru\; válce$
|
$Výpočet\; poloměru\; kužele$
|
| $V=\pi r^{2}\times v$
$r=\sqrt\frac{V}{\pi \times v}$ $r=\sqrt\frac{180}{\pi \times 15}$ $r=1,95\;cm$ |
$V=\frac{\pi r^{2}\times v}{3}$
$r=\sqrt\frac{3V}{\pi \times v}$ $r=\sqrt\frac{3\times 180}{\pi \times 15}$ $r=3,39\;cm$ |
|
|
|
| $Výpočet\; povrchu\; válce$
|
$Výpočet\; povrchu\; kužele$
|
| $S=\pi r^{2}+2\pi r v$
$S=\pi 1,95^{2}+2\pi\times 1,95 \times 15$ $S=207,7\;cm^{2}$ Větší povrch má válec. |
$Hrana\; kužele$
$s^{2}=r^{2}+v^{2}$ $s^{2}=3,39^{2}+15^{2}$ $s=15,4\;cm$ $S=\pi r^{2}+\pi r s$ $S=\pi 3,39^{2}+\pi \times 3,39 \times 15,4$ $S=200,1\;cm^{2}$ |
6. Vypočítej objem a povrch rotačního kužele o poloměru podstavy r = 23 cm a výšce v=4,6 cm.
$r=23\;cm$
$v=4,6\;cm$
| $Výpočet\; hrany$
|
$Povrch\;kužele$
|
$Objem$
|
|
$s^{2}=r^{2}+v^{2}$ $s^{2}=23^{2}+4,6^{2}$ $s=23,5\;cm$ |
$S=\pi r^{2}+\pi r s$
$S=\pi 23^{2}+\pi \times 23 \times 23,5$ $S=3359\;cm^{2}$ |
$V=\frac{\pi r^{2} \times v}{3}$
$V=\frac{\pi 23^{2} \times 4,6}{3}$ $V=2548\;cm^{3}$ |
7. Čtyřicet stejných dopravních kuželů s průměrem podstavy d = 36 cm a výškou v = 46 cm máme natřít zvenčí oranžovou barvou (bez podstavy). Kolik korun zaplatíme za barvu, pokud na natření 1 m2 potřebujeme 500 cm3 barvy a 1l barvy stojí 8 Kč?
$r=18\;cm$
$v=46\;cm$
| $Výpočet\; hrany$
|
$Povrch\;pláště\;kužele$
|
$Platba$
|
|
$s^{2}=r^{2}+v^{2}$ $s^{2}=18^{2}+46^{2}$ $s=49,4\;cm$ |
$S=\pi r s$
$S=\pi \times 18 \times 49,4$ $S=2794\;cm^{2}$ |
Celkový povrch
$40\; kuželů\; má\; plášť\; o\; povrchu \;2794\; \times \;40=111760\;cm^{2}=11,1760\;m^{2}$ Počet litrů barvy $11,1760\;m^{2} \times 0,5=5,588\;l$ Celková cena $5,588\times 8 = 44,7\;Kč$ |