1. Z jaké výšky může kosmonaut v každém okamžiku vidět 1 % povrchu země?
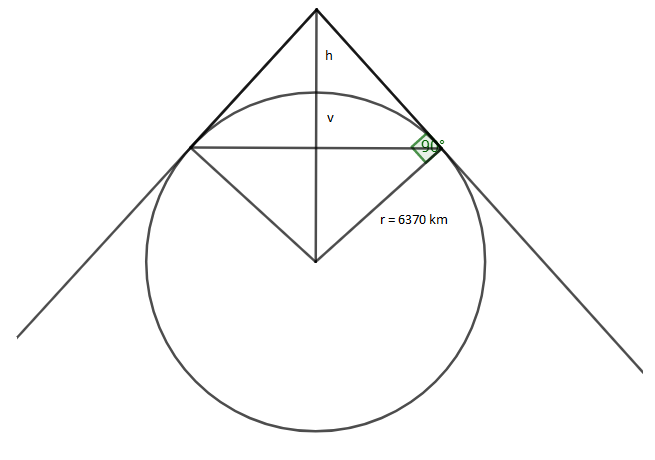
$S=4\pi r^{2}$
$r=6371\;km$
$S=509805891 \;km^{2}$
$0,01. S=5098058 \;km^{2}$ [1 % povrchu zeměkoule]
$S=2\pi rv$
$v=\frac{S}{2\pi r}$
$v=127,42\;km$ [výška vrchlíku, jehož povrch tvoří 1 % povrchu země]
$r^{2}=(r+h)(r-v)$
[vyjádříme h, vztah vychází z Euklidovy věty]
$r^{2}=r^{2}-rv+rh-vh$
$r^{2}=r^{2}-rv+rh-vh$
$rh-vh=rv$
$h(r-v)=rv$
$h=\frac{rv}{r-v}$
$h=\frac{6371.127,42}{6371-127,42}=130\;km$
2. Kolik procent povrchu země vidí pozorovatel z výšky 350 m nad zemí?
$S=4\pi r^{2}$
$S=509805891 \;km^{2}$
$r^{2}=(r+h)(r-v)$
$r^{2}=r^{2}-rv+rh-vh$
$r^{2}=r^{2}-rv+rh-vh$
$rv+vh=rh$
$v(r+h)=rh$
$v=\frac{rh}{r+h}$
$v=\frac{6371.0,35}{6371+0,35}$
$v=0,350\;km$
$S=2\pi rv$
$S=14003,5\;km^{2}$
$14003,5\; km^{2}\; tvoří\; 0,0027\; procenta \;z\; celkového\; povrchu země.$
3. Určete rozměry rovnostranného válce o objemu 1 l.
v = 2r
$V=\pi r^{2}v$
$V=\pi r^{2}2r$
$V=2 \pi r^{3}$
$r^{3}=\frac{1}{2 \pi}$
$r^{3}=0,1592$
$r=0,54\;dm$
$v=1,08\;dm$
4. Vypočítejte objem a povrch rotačního kužele o výšce 10 cm, jehož strana má od roviny podstavy odchylku $30^{o}$.
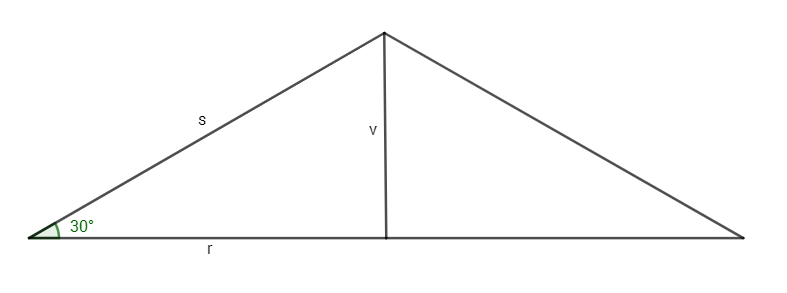
$sin\;30^{o}=\frac{v}{s}$
$s=\frac{v}{sin\;30^{o}}$
$s=20\;cm$
$cos\;30^{o}=\frac{r}{s}$
$r=cos\;30^{o}.s$
$s=17,32\;cm$
$V=\frac{\pi r^{2}.v}{3}$
$V=3139,82cm^{3}$
$S=\pi.r(r+s)$
$S=2029,64\;cm^{2}$
5. Vypočítejte kolik $m^{3}$ písku je v hromadě tvaru rotačního kužele s výškou 3,3 m a obvodem podstavy 18,85m.
$v=3,3\;m$
$O_{p}=18,85\;m$
$O_{p}=2 \pi r$
$r=\frac{O_{p}}{2 \pi}$
$r=3\;cm$
$V=\frac{\pi r^{2}.v}{3}$
$V=31,86\;cm^{3}$
5.72/180
Dva rotační válce mají výšky 64 cm a 27 cm. Plášť každého z nich má stejný obsah jako podstava druhého válce. V jakém poměru jsou objemy válců?
$Spl_{1}=2\pi r_{1}v_{1}$
$Sp_{1}=\pi r_{1}^{2}$
$Spl_{2}=2\pi r_{2}v_{2}$
$Sp_{2}=\pi r_{2}^{2}$
$2\pi r_{1}v_{1}=\pi r_{2}^{2}\;\;/\times v_{2}$
$2\pi r_{2}v_{2}=\pi r_{1}^{2}\;\;/\times v_{1}$
$2\pi r_{1}v_{1}\times v_{2}=\pi r_{2}^{2}\times v_{2}=V_{2}$
$2\pi r_{2}v_{2}\times v_{2}=\pi r_{1}^{2}\times v_{1}=V_{1}$
$\Large \frac{2\pi r_{1}v_{1}}{2\pi r_{2}v_{2}}=\frac{\pi r_{2}^{2}}{\pi r_{1}^{2}}$
$\Large \frac{r_{1}v_{1}}{r_{2}v_{2}}=\frac{r_{2}^{2}}{r_{1}^{2}}\;\;/\times \frac{r_{2}}{r_{1}}$
$\Large \frac{v_{1}}{v_{2}}=\frac{r_{2}^{3}}{r_{1}^{3}}$
$\Large \frac{r_{2}}{r_{1}}=\sqrt[3]{\frac{v_{1}}{v_{2}}}$
$\Large \frac{r_{2}}{r_{1}}=\sqrt[3]{\frac{64}{27}}$
$\Large \frac{r_{2}}{r_{1}}=\frac{4}{3}$
5.73/180
Osový řez nádoby, která má tvar rotačního válce, je obdélník s úhlopříčkou délky u = 39 cm. Poměr obsahu pláště a obsahu podstavy je 5:3. Kolik litrů vody se vejde do nádoby?
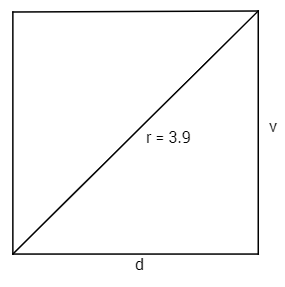
$\large \frac{2\pi r v}{\pi r^{2}}=\frac{5}{3}$
$\large \frac{2v}{r}=\frac{5}{3}$
$\large v=\frac{5r}{6}$
Poloměr a výšku dopočteme pomocí Pythagorovy věty:
$(2r)^{2}+(\frac{5r}{6})^{2}=39^{2}$
$4r^{2}+\frac{25r^{2}}{36}=39^{2}\;\;/\times 36$
$144r^{2}+25r^{2}=54756$
$169r^{2}=54756$
$r^{2}=324$
$r=18\;\;cm$
$v=15\;\;cm$
$V = \pi r^{2}v$
$V = \pi 324.15$
$V = 15260,4\;\;cm^{3}=15,3\;\;dm^{3}$
5.74/180
Jaké množství vody proteče za hodinu potrubím kruhového průřezu s průměrem 16 cm, teče-li voda rychlostí 2,5 m/s.
Za sekundu voda doteče 2,5 m, za hodinu doteče do vzdálenosti 9000 m.
$V= \pi r^{2}.v $
$V= \pi 0,08^{2}.9000$
$V=180,8640\; m^{3} \doteq 1809\;hl$
5.75/180
V podstavě rovnostranného válce poloměru r je vedena tětiva délky r. Rovina proložená touto tětivou rovnoběžně s osou válce rozdělí válec na dvě úseče. Určete objem a povrch větší z nich.
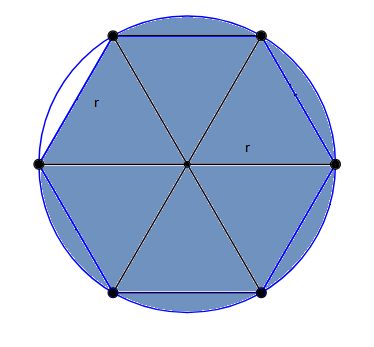
Objem tělesa spočítáme jako součin obsahu podstavy a výšky tělesa. Obsah podstavy vypočteme jako rozdíl šestiny obsahu kruhu o poloměru r a šestiny obsahu pravidelného šestiúhelníku o straně r.
$ S_{1}=\pi r^{2}\;\;\;obsah\; kruhu$
$ S_{2}=\frac{3\sqrt{3}r^{2}}{2}\;\;\;obsah\; šestiúhelníku$
$ S_{3}=\frac{\pi r^{2}}{6}-\frac{3\sqrt{3}r^{2}}{12}=\frac{2 \pi r^{2}-3\sqrt{3}r^{2}}{12}\;\;\;obsah\;bílé\;části\;kruhu$
$ S_{p}=\pi r^{2}-\frac{2 \pi r^{2}-3\sqrt{3}r^{2}}{12}=\frac{12\pi r^{2}-2\pi r^{2}-3\sqrt{3}r^{2}}{12}=\frac{10\pi r^{2}+3\sqrt{3}r^{2}}{12}\;\;\;obsah\;podstavy\;-\;modrá\;část$
Výška tělesa = 2r --> válec je rovnostranný
$\large V =\frac{2r(10\pi r^{2}+3\sqrt{3}r^{2})}{12} = \frac{10\pi r^{3}+3\sqrt{3}r^{3}}{6}=\frac{1}{6}r^{3}(10 \pi + 3\sqrt{3})$
Povrch tělesa tvoří $\frac{5}{6}$ pláště válce, obdélník na řezu válce a dvě podstavy.
$ S_{1}=\frac{5}{6}2 \pi r \times 2r$
$ S_{2}=2r^{2}$
$ S_{3}=\frac{2(10\pi r^{2}+3\sqrt{3}r^{2})}{12}=\frac{10\pi r^{2}+3\sqrt{3}r^{2}}{6}$
$\large S=\frac{20 \pi r^{2}}{6} + 2r^{2} + \frac{10\pi r^{2}+3\sqrt{3}r^{2}}{6}=\frac{30 \pi r^{2}}{6}+2r^{2}+\frac{\sqrt{3}r^{2}}{2}=5 \pi r^{2}+\frac{1}{2}+2r^{2}$
5.76/180
Vypočítejte objem šikmo seříznutého rotačního válce s průměrem podstavy 30 cm, mají-li jeho nejdelší a nejkratší strana délky 1,25 m a 1,05 m.
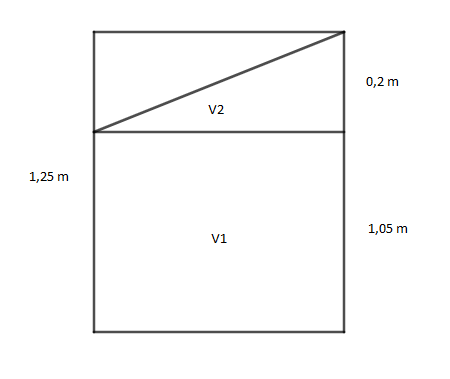
$V_{1}= \pi r^{2}v=3,14.0,15^{2}.1,05=0,0741825\;m^{3}=74,18\;l$
$V_{2}= \pi r^{2}v=3,14.0,15^{2}.0,2=0,014175\;m^{3}=14,18\;l$
$\large V=V_{1}+\frac{1}{2}V_{2}=74,18+7,09=81,27\;l$
5.79/181
Jak velký je středový úhel v rozvinutém plášti rovnoramenného kužele?
$s=2r$
$\alpha=\frac{2 \pi r}{s}=\frac{2 \pi r}{2r} =\pi = 180^{o}$
5.80/181
Vypočtěte obsah lampového stínítka tvaru rotačního komolého kužele s průměry podstav 32 cm a 12 cm a výškou 24 cm. Jaký je úhel výseče mezikruží, z něhož stínítko vzniklo?
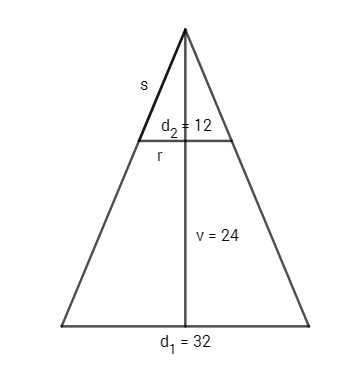
Pro výpočet úhlu potřebujeme znát velikost úsečky s. Proto musíme zjistit výšku menšího trojúhelníku využitím podobnosti trojúhelníků: poměr výšek je shodný s poměrem poloměrů obou podobných trojúhelníků.
$\frac{v}{v-24}=\frac{R}{r}$
$vr=Rv-24R$
$v(r-R)=-24R$
$v=\frac{-24R}{r-R}$
$\large v=\frac{24R}{R-r}$
$v=\frac{24.16}{16-6}$
$v=38,4\;cm$
Celková výška je 38,4 cm. Stranu s (přeponu) vypočítáme pomocí Pythagorovy věty. Odvěsny mají délky r=6 cm a v = 38,4-24=14,4 cm.
$s^{2}=6^{2}+14,4^{2}$
$s=15,6\;cm$
$\large \alpha=\frac{2\pi 6}{15,6}=138^{o}28^{'}$
Výpočet hrany stínítka pomocí Pythagorovy věty:
$s=\sqrt{(16-6)^{2}+24^{2}}$
$s=26 cm$
Výpočet plochy stínítka:
$S= \pi (r_{1}+r_{2}).s$
$S= 3,14.22.26$
$\large S= 1796\; cm^{2}$
Zdroj: POMYKALOVÁ, Eva. Matematika pro gymnázia: stereometrie. 3. upr. vyd. Praha: Prometheus, 2000. Učebnice pro střední školy. ISBN 80-7196-178-7.