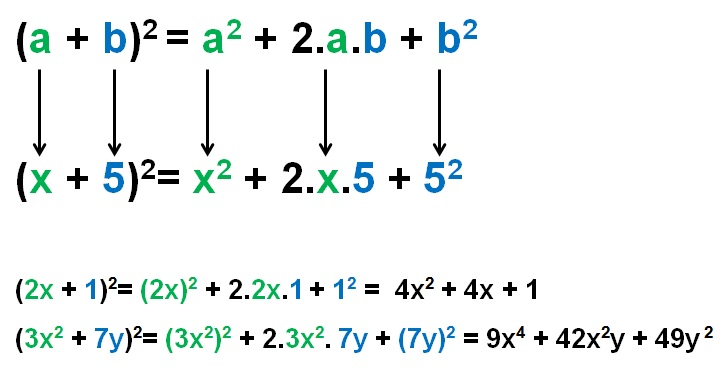Výrazy, v nichž se vyskytují pouze reálná čísla, jsou číselné výrazy.
Výrazy obsahující aspoň jednu proměnnou jsou algebraické výrazy.
Algebraické výrazy, v nichž se proměnná nevyskytuje ve jmenovateli, se nazývají celistvé výrazy.
Dosadíme-li do daného výrazu za proměnné reálná čísla, je výsledkem číslo, které se nazývá číselná hodnota výrazu.
Zápis algebraických výrazů - online test
Zápis algebraických výrazů - pdf ke stažení
Celistvé výrazy $9x, 2x - 3, 3x^{2}+2x+5$ se nazývají mnohočleny.
Mnohočleny mohou mít i více proměnných $2xy - 3x, 3x^{2}y+5yz+6z-7$.
Podle počtu členů rozlišujeme:
-
jednočleny $9x, 3x^{2}, 0,25k$;
-
dvojčleny $2x + 3, 3x^{2}-5x,2ab - b^{2}$;
-
trojčleny $6x^{2}-5x +1,\frac{4x^{2}}{9} - x^{2} + 1$;
-
atd.
Sčítání a odčítání celistvých výrazů - online test
Sčítání a odčítání celistvých výrazů - pdf ke stažení
Při násobení výrazů postupujeme tak, že každý člen jednoho výrazu vynásobíme každý člene druhého výrazu.

Pro každé reálné číslo a a každé přirozené číslo m, n platí, že:
$a^{m} \times a^{n} = a^{m+n}$
$3^{2} \times 3^{5} = 3^{2+5}=3^{2+5}$
Násobení výrazů - online test
Násobení výrazů - pdf ke stažení
Výrazy na součin upravujeme vytýkáním před závorku a pomocí vzorců. Vytýkání před závorku je opačná operace k roznásobování závorek.
$6x^{2}y - 3xy$
Z obou členů výrazu můžeme vytknout 3xy.
$3xy(2x - 1)$
Když závorku znovu roznásobíme, musíme dostat původní zadání - hodnota výrazu vytknutím se nezmění.
Rozklad na součin vytýkáním - online cvičení
Rozklad na součin vytýkáním - pdf ke stažení
Vzorce
$(a+b)^{2}=a^{2}+2ab+b^{2}$
$(a-b)^{2}=a^{2}-2ab+b^{2}$
$a^{2}-b^{2}=(a+b)(a-b)$
$(a+b)^{3}=a^{3}+3a^{2}b+3ab^{2}+b^{3}$
$(a-b)^{3}=a^{3}-3a^{2}b+3ab^{2}-b^{3}$
$a^{3}+b^{3}=(a+b)(a^{2}-ab+b^{2})$
$a^{3}-b^{3}=(a-b)(a^{2}+ab+b^{2})$
Postup při dosazování do vzorce