Přímá úměrnost

O dvou veličinách prohlásíme, že jsou přímo úměrné, jestliže bude platit, že když jednu veličinu zvětšíme (zmenšíme) x krát, tak druhou veličinu zvětšíme ( zmenšíme ) také x krát.
Ve vztahu přímé úměrnosti jsou například veličiny :
- množství jablek a jejich celková cena (Při stejné ceně za 1 kg: Čím více jablek koupíme, tím více peněz zaplatíme.),
- rychlosti a ujeté dráhy (Při stejné době: Čím větší bude rychlost auta, tím větší vzdálenost ujedeme.),
- času a ujeté dráhy (Při stejné rychlosti: Za delší čas ujedeme delší vzdálenost.),
- poloměru kružnice a délky kružnice (Čím větší bude poloměr, tím větší bude obvod kružnice.).
Jak funguje přímá úměrnost můžeme vyčíst z grafu. Čím více jablek koupíme, tím více zaplatíme - jednomu kilogramu odpovídá 25 Kč, třem kilogramům 75 Kč. Pokud je množství jablek X a celková zaplacená cena Y pak platí, že $y = 25 . x$.
Nepřímá úměrnost
O dvou veličinách prohlásíme, že jsou nepřímo úměrné, jestliže bude platit, že když jednu veličinu zvětšíme (zmenšíme) x krát, tak druhou veličinu zmenšíme (zvětšíme) také x krát.
Ve vztahu nepřímé úměry jsou například veličiny :
- čas a rychlost vozidla potřebné k ujetí dané vzdálenosti (Čím větší bude rychlost, tím kratší bude potřebný čas.),
- délka a šířka obdélníka (Při stejném obsahu: Čím větší bude délka, tím kratší bude šířka.),
- čas a počet stejně výkonných pracovníků k udělání konkrétní práce. (Více dělníků udělá práci za kratší čas.)
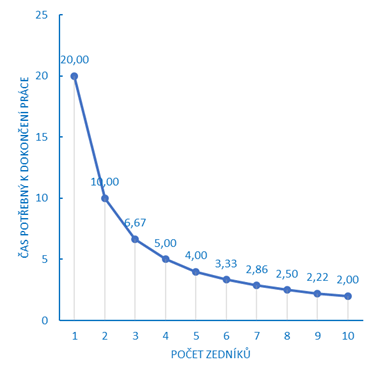
V grafu opět vidíme, jak s větším počtem zedníků klesá čas potřebný k dokončení práce. Jeden zedník vykoná práci za 20 hodin a deset zedníků udělá stejnou práci za dvě hodiny. Když počet zedníků bude X a čas potřebný k dokončení práce Y, pak $y = \frac{20}{x}$.
Příklady na úměrnost
1.Šest stejných hrnečků stojí 54 Kč. Kolik stojí 20 takových hrnečků?
Čím více hrnečků, tím více peněz zaplatíme. PŘÍMÁ ÚMĚRA
|
$\huge\uparrow$
|
6 hrnečků
|
54 Kč
|
$\huge\uparrow$
|
| 20 hrnečků
|
x Kč
|
Podrobný postup:
Šipku začínáme psát vedle neznámé x. Pokud se jedná o přímou úměru, tak šipka na druhé straně tabulky jde stejným směrem. Když máme nepřímou úměru zapíšeme šipku opačným směrem.
Podle tabulky sestavíme rovnici podle šipek a začneme vždy od neznámé x.
$\Large \frac{x}{54}=\frac{20}{6}$
$\large x=\frac{20}{6} \times 54$
$\large x=180$
Za 20 hrnečků zaplatíme 180 Kč.
Kontrola: Hrnečků jsme chtěli koupit zhruba třikrát tolik, takže musíme i zhruba třikrát tolik zaplatit. Třikrát 50 je 150, takže náš výsledek 180 bude správný. Pokud by nám vyšel výrazně odlišný výsledek (např. 16 Kč nebo 1800 Kč), máme ve výpočtu s největší pravděpodobností chybu. Vždy doporučuji u všech slovních úloh se nad výsledkem zamyslet, zda je reálný.
2.Ze 2 kg švestek se získá 600 g povidel. Kolik povidel se získá ze 3,2 kg švestek?
Čím více švestek, tím více povidel. PŘÍMÁ ÚMĚRA
|
$\huge\uparrow$
|
2 kg švestek
|
600 g povidel
|
$\huge\uparrow$
|
| 3,2 kg švestek
|
x g povidel
|
$\Large \frac{x}{600}=\frac{3,2}{2}$
$\large x=\frac{3,2}{2} \times 600$
$\large x=960$
Ze 3,2 kg švestek získáme 960 g povidel.
3.Hodinky se zpožďují o 20 sekund za 4 dny. O kolik se zpozdí za týden?
Čím více dnů, tím více sekund zpoždění. PŘÍMÁ ÚMĚRA
|
$\huge\uparrow$
|
4 dny
|
20 sekund
|
$\huge\uparrow$
|
| 7 dní
|
x sekund
|
$\Large \frac{x}{20}=\frac{7}{4}$
$\large x=\frac{7}{4} \times 20$
$\large x=35$
Za týden (7 dní) se hodinky zpozdí o 35 sekund.
4.Za kolik minut urazí cyklista dráhu 8,125 km průměrnou rychlostí 12,5 km/hod?
Čím více minut cyklista pojede, tím větší vzdálenost urazí při stejné průměrné rychlosti. PŘÍMÁ ÚMĚRA
|
$\huge\uparrow$
|
12,5 km
|
60 minut
|
$\huge\uparrow$
|
| 8,125 km
|
x minut
|
$\Large \frac{x}{60}=\frac{8,125}{12,5}$
$\large x=\frac{8,125}{12,5} \times 60$
$\large x=39$
Dráhu 8,125 km urazí cyklista za 39 minut.
5.Cyklista urazí danou dráhu průměrnou rychlostí 15 km/hod za 4 hodiny.
a) Jakou průměrnou rychlostí urazí danou dráhu za 3 hodiny?
Čím větší rychlost, tím kratší čas. Aby dosáhl cyklista kratšího času, musí jet rychleji. NEPŘÍMÁ ÚMĚRA
|
$\huge\downarrow$
|
4 hodiny
|
15 km/hod
|
$\huge\uparrow$
|
| 3 hodiny
|
x km/hod
|
$\Large \frac{x}{15}=\frac{4}{3}$
$\large x=\frac{4}{3} \times 15$
$\large x=20$
Cyklista musí jet rychlostí 20 km/hod.
b) Za jak dlouho ujede danou dráhu průměrnou rychlostí 25 km/hod?
Čím větší rychlost, tím kratší čas. Aby dosáhl cyklista kratšího času, musí jet rychleji. NEPŘÍMÁ ÚMĚRA
|
$\huge\uparrow$
|
4 hodiny
|
15 km/hod
|
$\huge\downarrow$
|
| x hodin
|
25 km/hod
|
$\Large \frac{x}{4}=\frac{15}{25}$
$\large x=\frac{15}{25} \times 4$
$\large x=2,4$
Cyklista rychlostí 25 km/hod ujede dráhu za 2,4 hodiny, tj. 2 hodiny a 24 minut.
Poznámka: 0,4 hodiny jsou čtyři desetiny a jedna desetina z 60 minut je 6 minut. Čtyři desetiny jsou tedy 24 minut.
6.Čerpadlem o výkonu 25 litrů za sekundu se nádrž naplní za 1 hodinu 12 minut. Jak dlouho bude trvat naplnění nádrže čerpadlem o výkonu 20 litrů za sekundu?
Čím větší výkon čerpadla, tím kratší čas potřebný pro naplnění nádrže. NEPŘÍMÁ ÚMĚRA
|
$\huge\downarrow$
|
25 litrů/s
|
1 hod a 12 minut (1,2)
|
$\huge\uparrow$
|
| 20 litrů/s
|
x minut
|
$\Large \frac{x}{1,2}=\frac{25}{20}$
$\large x=\frac{25}{20} \times 1,2$
$\large x=1,5$
Čerpadlem o výkonu 20 litrů/s bude naplnění nádrže trvat 1 hodinu a 30 minut.
Poznámka: 0,5 hodiny je pět desetin a jedna desetina z 60 minut je 6 minut. Pět desetin je tedy 30 minut. 0,5 je jedna polovina a polovina z hodiny je 30 minut.
7.Ubytování v hotelu stojí 18 000 Kč za 10 dní. Kolik se zaplatí za týden?
Čím více dnů, tím více peněz za ubytování. PŘÍMÁ ÚMĚRA
|
$\huge\uparrow$
|
10 dní
|
18 000 Kč
|
$\huge\uparrow$
|
| 7 dní
|
x Kč
|
$\Large \frac{x}{18000}=\frac{7}{10}$
$\large x=\frac{7}{10} \times 18000$
$\large x=12600$
Týden ubytování bude stát 12 600 Kč.
8.Osmnáct metrů látky stojí 720 Kč. Kolik zaplatíme za 12 m téže látky? Kolik látky koupíme za 900 Kč?
Čím více metrů látky, tím více peněz zaplatíme. PŘÍMÁ ÚMĚRA
|
$\huge\uparrow$
|
18 m
|
720 Kč
|
$\huge\uparrow$
|
| 12 m
|
x Kč
|
$\Large \frac{x}{720}=\frac{12}{18}$
$\large x=\frac{12}{18} \times 720$
$\large x=480$
Za 12 m látky zaplatíme 480 Kč.
|
$\huge\uparrow$
|
18 m
|
720 Kč
|
$\huge\uparrow$
|
| x m
|
900 Kč
|
$\Large \frac{x}{18}=\frac{900}{720}$
$\large x=\frac{900}{720} \times 18$
$\large x=22,5$
Za 900 Kč koupíme 22,5 m látky.
9.Čerpadlem o výkonu 25 litrů za sekundu se naplní nádrž za 1 hodinu a 12 minut. Za jak dlouho se naplní nádrž čerpadlem o výkonu 10 litrů za sekundu?
Čím větší výkon čerpadla, tím kratší čas potřebný pro naplnění nádrže. NEPŘÍMÁ ÚMĚRA
|
$\huge\downarrow$
|
25 litrů/s
|
1 hod a 12 minut
|
$\huge\uparrow$
|
| 10 litrů/s
|
x minut
|
Poznámka: 6 minut je jedna desetina z hodiny, 12 minut jsou dvě desetiny. 1 hodina a 12 minut je 1,2 hodiny.
$\Large \frac{x}{1,2}=\frac{25}{10}$
$\large x=\frac{25}{10} \times 1,2$
$\large x=3$
Čerpadle o výkonu 10 litrů/s se nádrž naplní za 3 hodiny.
10.Automat vyrobí za 18 minut 456 součástek. Kolik jich vyrobí za 33 minut?
Čím více minut, tím více součástek. PŘÍMÁ ÚMĚRA
|
$\huge\uparrow$
|
18 minut
|
456 součástek
|
$\huge\uparrow$
|
| 33 minut
|
x součástek
|
$\Large \frac{x}{456}=\frac{33}{18}$
$\large x=\frac{33}{18} \times 456$
$\large x=836$
Za 33 minut se vyrobí 836 součástek.
11.Ubytování v ubytovně stojí pro dvě osoby ve dvoulůžkovém pokoji na 1 noc a den 175 Kč. Kolik Kč zaplatí čtyřčlenná rodina za 5 dnů pobytu?
Čím více dnů pobytu, tím více peněz. PŘÍMÁ ÚMĚRA
|
$\huge\uparrow$
|
2 osoby/noc
|
175 Kč
|
$\huge\uparrow$
|
| 4 osoby/noc
|
x Kč
|
$\Large \frac{x}{175}=\frac{4}{2}$
$\large x=\frac{4}{2} \times 175$
$\large x=350$
Čtyři osoby zaplatí za jednu noc 350 Kč, za čtyři noci zaplatí 4 * 350 Kč, to je 1400 Kč.
12.Autobus ujede 4 km za 7 minut. Kolik minut pojede do místa vzdáleného 28 km, nebude-li cestou stavět?
Čím více minut, tím více kilometrů ujede stejnou průměrnou rychlostí. PŘÍMÁ ÚMĚRA
|
$\huge\uparrow$
|
4 km
|
7 minut
|
$\huge\uparrow$
|
| 28 km
|
x minut
|
$\Large \frac{x}{7}=\frac{28}{2}$
$\large x=\frac{28}{2} \times 7$
$\large x=49$
Autobus urazí 28 km za 49 minut.
13.V prodejně stojí 2,4 kg hovězího masa 292,80 Kč. Kolik korun stojí 7,5 kg hovězího masa stejného druhu v této prodejně? Kolik hovězího masa stejného druhu zde koupím za 1 000 Kč?
Čím více masa, tím více peněz. PŘÍMÁ ÚMĚRA
|
$\huge\uparrow$
|
2,4 kg
|
292,80 Kč
|
$\huge\uparrow$
|
| 7,5 kg
|
x Kč
|
$\Large \frac{x}{292,80}=\frac{7,5}{2,4}$
$\large x=\frac{7,5}{2,4} \times 292,80$
$\large x=915$
Za 7,5 kg masa zaplatíme 915 Kč.
|
$\huge\uparrow$
|
2,4 kg
|
292,80 Kč
|
$\huge\uparrow$
|
| x kg
|
1000 Kč
|
$\Large \frac{x}{2,4}=\frac{1000}{292,80}$
$\large x=\frac{1000}{292,80} \times 2,4$
$\large x=8,2$
Za 1000 Kč koupíme 8,2 kg.
14.Turista ujde 1 km za 12 minut. Kolik km ujde za 2,5 hodiny?
Čím více času, tím více kilometrů turista ujde. PŘÍMÁ ÚMĚRA
|
$\huge\uparrow$
|
12 minut
|
1 km
|
$\huge\uparrow$
|
| 150 minut
|
x km
|
$\Large \frac{x}{1}=\frac{150}{12}$
$\large x=\frac{150}{12} \times 1$
$\large x=12,5$
Za 2,5 hodiny ujde turista 12,5 km.
15.Do ozubeného kola o 36 zubech zapadá jiné kolo o 20 zubech. Kolikrát se otočí druhé kolo, otočí-li se prvé desetkrát?
Čím více zubů, tím méně otáček. NEPŘÍMÁ ÚMĚRA
|
$\huge\downarrow$
|
36 zubů
|
10 otáček
|
$\huge\uparrow$
|
| 20 zubů
|
x otáček
|
$\Large \frac{x}{10}=\frac{36}{20}$
$\large x=\frac{36}{20} \times 10$
$\large x=18$
Kolo s 20 zuby se otočí osmnáctkrát.
16.Prázdná nádoba má hmotnost 4,6 kg. Naplněná olejem 26,68 kg. Kolik litrů oleje je v nádobě, když jeden litr oleje má hmotnost 920 gramů?
Čím větší objem, tím více kilogramů oleje. PŘÍMÁ ÚMĚRA
26,68 kg - 4,6 kg = 22,08 kg
Od hmotnosti nádoby s olejem odečteme hmotnost prázdné nádoby. Hmotnost oleje v nádobě je 22,08 kg, tj. 22 080 g.
22 080 : 920 = 24 l
Hmotnost oleje podělíme hmotností jednoho litru oleje. Zjistíme kolikrát "se vejde" hmotnost litru oleje do námi vypočtené hmotnosti.
Hmotnost 22,08 kg představuje 24 litrů oleje.
17.Jeden kilogram má hmotnost 165 kostek cukru. Kolik kostek má hmotnost 70 gramů? Jakou hmotnost má 1 000 kostek cukru?
Více kostek cukru má větší hmotnost. PŘÍMÁ ÚMĚRA
|
$\huge\uparrow$
|
1000 g
|
165 kostek cukru
|
$\huge\uparrow$
|
| 70 g
|
x kostek cukru
|
$\Large \frac{x}{165}=\frac{70}{1000}$
$\large x=\frac{70}{1000} \times 165$
$\large x=11,55$
Sedmdesát gramů váží 11,55 kostek cukru.
|
$\huge\uparrow$
|
1000 g
|
165 kostek cukru
|
$\huge\uparrow$
|
| x g
|
1000 kostek cukru
|
$\Large \frac{x}{1000}=\frac{1000}{165}$
$\large x=\frac{1000}{165} \times 1000$
$\large x=6060,60$
Tisíc kostek cukru váží 6060,6 g.
18.Ze dvou ozubených kol zapadajících do sebe má jedno 42 zubů, druhé 119 zubů. Kolikrát se otočí prvé, otočí-li se druhé 12 krát?
Čím více zubů, tím méně otáček. NEPŘÍMÁ ÚMĚRA
|
$\huge\uparrow$
|
42 zubů
|
x otáček
|
$\huge\downarrow$
|
| 119 zubů
|
12 otáček
|
$\Large \frac{x}{12}=\frac{119}{42}$
$\large x=\frac{12}{42} \times 119$
$\large x=43$
Kolo s 42 zuby se otočí o 43 otáček..
19.Za tři čtvrtě hodiny pokryl zedník obkládačkami tři pětiny zdi kolem umyvadla. Za jak dlouho obložil celou zeď kolem umyvadla?
Čím více času, tím více práce. PŘÍMÁ ÚMĚRA
Poznámka: Tři čtvrtě hodiny je 45 minut. Jedna pětina je 20 % práce, tři pětiny jsou 60 % práce.
|
$\huge\uparrow$
|
45 minut
|
60 procent práce
|
$\huge\uparrow$
|
| x minut
|
100 procent práce
|
$\Large \frac{x}{45}=\frac{100}{60}$
$\large x=\frac{100}{60} \times 45$
$\large x=75$
Celou zeď obloží zedník za 75 minut, zbývá mu tedy ještě 30 minut práce.
20.Malíř zvětšoval obrázek o rozměrech 9 cm a 7 cm. Jakou šířku bude mít zvětšený obrázek, jestliže jeho délka bude 16,2 cm?
Čím větší jedna strana, tím většíi druhá strana obrázku. PŘÍMÁ ÚMĚRA
|
$\huge\uparrow$
|
9 cm
|
16,2 cm
|
$\huge\uparrow$
|
| 7 cm
|
x cm
|
$\Large \frac{x}{16,2}=\frac{7}{9}$
$\large x=\frac{7}{9} \times 16,2$
$\large x=12,6$
Obrázek bude mít po zvětšení šírku 12,6 cm.
Složitější úlohy na úměrnost
1. Z bazénu vyteče 100 hl vody 3 rourami za 8 hodin. Kolik litrů vody vyteče 4 stejně velkými rourami za 10 hodin?
|
$\huge\uparrow$
|
100 hl | 3 roury | 8 h |
$\huge\uparrow$
|
| x hl
|
3 roury | 10 h
|
$\Large \frac{x}{100}=\frac{10}{8}$
$\large x=\frac{100}{8} \times 10$
$\large x=125$
Za 10 hodin proteče třemi rourami 125 hl.
|
$\huge\downarrow$
|
x hl | 4 roury | 10 h |
$\huge\downarrow$
|
| 125 hl
|
3 roury | 10 h
|
$\Large \frac{x}{125}=\frac{4}{3}$
$\large x=\frac{125}{3} \times 4$
$\large x=166,67$
Za 10 hodin proteče čtyřmi rourami 166,67 hl.
2. Šest švadlen ušije 5 obleků za 3 dny. Za jak dlouho ušijí 4 švadleny 8 obleků?
|
$\huge\uparrow$
|
6 švadlen | 5 obleků | 3 dny |
$\huge\uparrow$
|
| 6 švadlen | 8 obleků | x dnů |
$\Large \frac{x}{3}=\frac{8}{5}$
$\large x=\frac{8}{5} \times 3$
$\large x=4,8$
|
$\huge\uparrow$
|
4 švadleny | 8 obleků | x dnů |
$\huge\downarrow$
|
| 6 švadlen | 8 obleků | 4,8 dne |
$\Large \frac{x}{4,8}=\frac{6}{4}$
$\large x=\frac{6}{4} \times 4,8$
$\large x=7,2$
Čtyři švadleny ušijí 8 obleků za 7,2 dny.
3. Tři truhláři vyrobili za 6,5 hodiny 24 stolů. Udělají tuto práci také čtyři truhláři při stejném výkonu za 5 hodin?
|
$\huge\uparrow$
|
3 truhláři | 6,5 hodiny | 24 stolů |
$\huge\uparrow$
|
| 4 truhláři | 6,5 hodiny | x stolů |
$\Large \frac{x}{24}=\frac{4}{3}$
$\large x=\frac{4}{3} \times 24$
$\large x=32$
|
$\huge\uparrow$
|
4 truhláři | 6,5 hodiny | 32 stolů |
$\huge\uparrow$
|
| 4 truhláři | 5 hodin | x stolů |
$\Large \frac{x}{32}=\frac{5}{6,5}$
$\large x=\frac{5}{6,5} \times 32$
$\large x=24,62$
Čtyři truhláři za 5 hodin zvládnou vyrobit 24 stolů.
4. Jarní setbu provede 9 traktorů při patnácti hodinové pracovní době za 8 dní. Protože deště zdržely setbu družstvo nasadilo 12 stejně výkonných traktorů, které pracovali 18 hodin denně. Za kolik dní provedou setbu?
|
$\huge\downarrow$
|
9 traktorů | 15 hodin * 8 dní | 120 hodin |
$\huge\uparrow$
|
| 12 traktorů | 18 hodin * x dní | 18x hodin |
$\Large \frac{18x}{120}=\frac{9}{12}$
$\large 18x \times 12=9 \times 120$
$\large 216x=1080$
$\large x=5$
Setbu provedou za 5 dní.
5. Traktorista zapojil za traktor 2 secí stroje a zasel za 5 hodin 7 ha žita. Kolik hektarů zasel za 8 hodin příští den, jestliže zapojil 3 secí stroje?
|
$\huge\uparrow$
|
2 secí stroje | 5 hodin | 7 ha |
$\huge\uparrow$
|
| 3 secí stroje | 5 hodin | x ha |
$\Large \frac{x}{7}=\frac{3}{2}$
$\large x=\frac{3}{2} \times 7$
$\large x=10,5$
|
$\huge\uparrow$
|
3 secí stroje | 5 hodin | 10,5 ha |
$\huge\uparrow$
|
| 3 secí stroje | 8 hodin | x ha |
$\Large \frac{x}{10,5}=\frac{8}{5}$
$\large x=\frac{8}{5} \times 10,5$
$\large x=16,8$
Tři secí stroje posečou za 8 hodin 16,8 hektarů.