Soustavu dvou rovnic o dvou neznámých můžeme řešit různými metodami.
dosazovací metoda
sčítací metoda
srovnávací metoda
grafické řešení
1. Dosazovací metoda
Z jedné rovnice vyjádříme neznámou.
$3x-4y=20$
$\underline {x+3y=-2 \;\; \rightarrow \;\; x=-2-3y}$
Výraz dosadíme do druhé rovnice, tím se zbavíme jedné proměnné (x) a můžeme jednoduše vypočítat proměnnou y.
$3\times(-2-3y)-4y=20$
$-6-9y-4y=20$
$-13y=26$
$y=-2$
Dosadíme výsledek do zadání $x=-2-3y$
$x=-2-3\times(-2)$
$x=-2+6$
$x=4$
$P=[x;y]=[4;-2]$
2. Sčítací metoda
Jednu nebo obě rovnice vhodně vynásobíme tak, abychom vyloučili jednu neznámou.
$2x+5y=3\;\;/\times\;(-5)$
$\underline {10x+7y=-3\;\;}$
$-10x-25y=-15$
$\underline {10x+7y=-3\;\;}$
Rovnice sečteme.
$-18y=-18$
$y=1$
Dosadíme výsledek do zadání.
$2x+5\times (1)=3$
$2x+5=3$
$2x=3-5$
$2x=-2$
$x=-1$
$P=[x;y]=[-1;1]$
3. Srovnávací metoda
Z obou rovnic vyjádříme neznámou.
$x+y=1\;\; \rightarrow \;\; x=1-y$
$\underline {x-2y=-14 \;\; \rightarrow \;\; x=-14+2y}$
Výrazy pro proměnnou x se musí rovnat.
$1-y=-14+2y$
$-y-2y=-14-1$
$-3y=-15$
$y=5$
Dosadíme výsledek do zadání.
$x=1-5$
$x=-4$
$P=[x;y]=[-4;-5]$
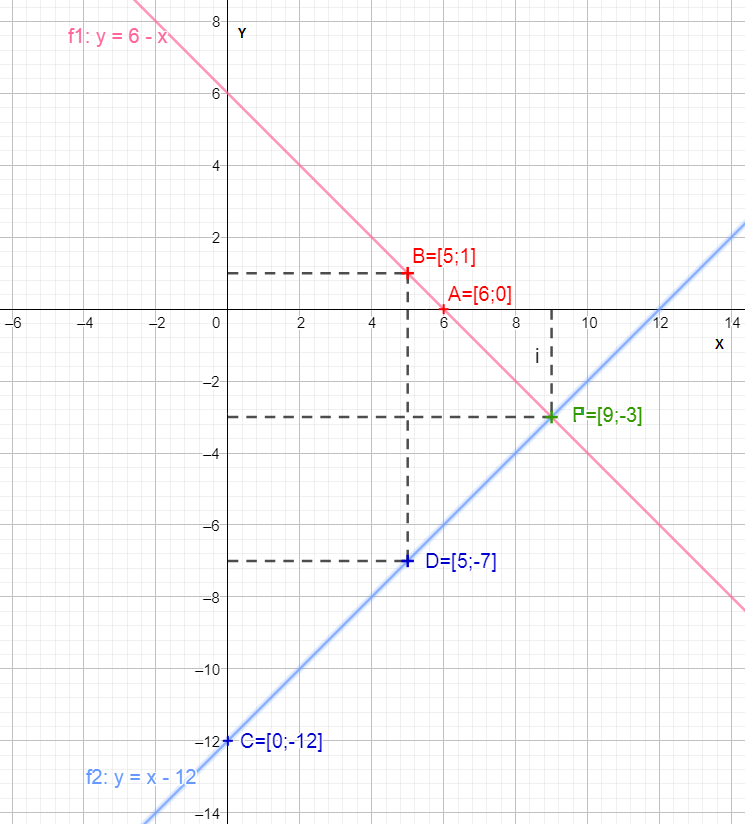
4. Grafická metoda
Hledáme uspořádanou dvojici [x;y], která vyhovuje oběma rovnicím.
$x+y=6\;\; \rightarrow \;\;\mathbf {y=6-x}$
$\underline {-x+y=-12 \;\; \rightarrow \;\;\mathbf {y=x-12}}$
Zvolíme libovolné hodnoty x a vypočítáme y.
| $x$
|
0
|
5
|
| $y=6-x$
|
6
|
1
|
| $x$
|
0
|
5
|
| $y=x-12$
|
-12
|
-7
|
Zakreslíme do grafu.
$P=[x;y]=[9;-3]$