Slovní úlohy na pohyb většinu studentů vyloženě děsí. Přitom pokud zvolíme správný systematický postup není vyřešení jednoduchých a středně obtížných úloh až tak náročné.
Jak tedy na slovní úlohy o pohybu?
1. Základem řešení všech slovních úloh je pozorné přečtení zadání, lépe vícekrát než jednou.
2. Dalším krokem je náčrtek situace, o které se ve slovní úloze mluví. Nejčastěji se jedná o "potkávačku", kdy se dva objekty pohybují proti sobě a někde "mezi" se potkají. Druhým nejčastějším typem je "doháněčka", kdy rychleji pohybující se objekt dohoní objekt, který vyjel dříve.
Toto naše zhodnocení situace rozhodne, zda se budou dráhy obou objektů rovnat ($s_{1} = s_{2}$) nebo zda jejich součet bude tvořit dráhu celkovou ($s = s_{1} + s_{2}$).
3. Po provedení této analýzy situace zapíšeme hodnoty do tabulky. Jednotlivé dráhy, které se buď rovnají nebo jejich součet je celkovou dráhou, se vypočítají jako součin rychlosti a času.
4. Na základě tabulky vytvoříme rovnici, kterou vypočítáme. Poté většinou musíme převést zlomek na časový údaj. A máme hotovo :-).
Slovní úlohy na pohyb
Neznámá t je čas v hodinách. Z rovnice vypočítej neznámou a výsledek uveď v hodinách a minutách.
- 20t = 50
- 5t = 28
- 12t = 19
- 30t = 134
- 18t = 69
$20t = 50$
$Pomocný výpočet : \frac{1}{2}\: z \:60\: minut = 30\: minut$
$t = \frac{5}{2}=2\frac{1}{2} = 2\: hodiny\: a\: 30\: minut$
$5t = 28$
$Pomocný výpočet : \frac{1}{5}\: z \:60\: minut = 12\: minut$
$t = \frac{28}{5}=5\frac{3}{5} = 5\: hodin\: a\: 36\: minut$
$12t = 19$
$Pomocný výpočet : \frac{1}{12}\: z \:60\: minut \:= \:5\: minut$
$t = \frac{19}{12}=1\frac{7}{12} = 1\: hodina\: a\: 35\: minut$
$30t = 134$
$15t = 67$
$Pomocný výpočet : \frac{1}{15}\: z\: 60\: minut = 4\: minuty$
$t = \frac{67}{15}=4\frac{7}{15} = 4\: hodiny\: a\: 28\: minut$
$18t = 69$
$6t = 23$
$Pomocný výpočet : \frac{1}{6}\: z\: 60\: minut = 10\: minut$
$t = \frac{23}{6}=3\frac{5}{6} = 3\: hodiny\: a\: 50\: minut$
1. Vzdálenost z Prahy do Olomouce je přibližně 250 km. V 6.00 vyjel z Prahy do Olomouce rychlík rychlostí 85 km/h. Ve stejném okamžiku mu vyjel naproti z Olomouce osobní vlak rychlostí 65 km/h. za jak dlouho se vlaky setkají?
|
|
rychlost [v]
|
čas [t]
|
s = v . t
|
|---|---|---|---|
| 1. objekt A - rychlík
|
85 km/h
|
t hod
|
85.t km
|
| 2. objekt B - osobní vlak
|
65 km/h
|
t hod
|
65.t km
|
| celkem
|
|
|
250 km
|
$s = s_{1}+ s_{2}$
$250 = 85t + 65t$
$250 = 150t$
$t = \frac{5}{3} = 1\frac{2}{3}$
Vlaky se setkají za 1 hodinu a 40 minut.
2. Dvě letadla startující současně z letišť A a B letí navzájem proti sobě a setkají se za 20 minut. Vzdálenost letišť je 220 km a průměrná rychlost letadla letícího z letiště A je o 60 km/h větší než průměrná rychlost druhého letadla. Vypočítej průměrné rychlosti obou letadel.
|
|
rychlost [v]
|
čas [t]
|
s = v . t
|
|---|---|---|---|
| 1. objekt A - letadlo
|
v km/h
|
$\frac{1}{3}$ hod
|
$\frac{x}{3}$ km
|
| 2. objekt B - letadlo
|
(v + 60) km/h
|
$\frac{1}{3}$ hod
|
$\frac{x+60}{3}$ km
|
| celkem
|
|
|
220 km
|
$s = s_{1}+ s_{2}$
$220 = \frac{v}{3} + \frac{v+60}{3}$
$660 = v + v + 60$
$2v = 600$
$v = 300$
Letadla letí rychlostí 300 km/h a 360 km/h.
3. Vzdálenost míst A a B je 132 km. V 9.00 vyjel z místa A cyklista průměrnou rychlostí 24 km/h, v 10.00 h mu vyjel naproti druhý cyklista průměrnou rychlostí 30 km/h. Za jak dlouho a jak daleko od místa A se oba setkají?
|
|
rychlost [v]
|
čas [t]
|
s = v . t
|
|---|---|---|---|
| 1. objekt A - cyklista
|
24 km/h
|
t hod
|
24.t km
|
| 2. objekt B - cyklista
|
30 km/h
|
(t-1) hod
|
30(t-1) km
|
| celkem
|
|
|
132 km
|
$s = s_{1}+ s_{2}$
$132 = 24t + 30(t-1)$
$132 = 24t + 30t - 30$
$162 = 54t $
$t = 3$
Cyklisté se potkají za 3 hodiny od startu prvního cyklisty. Za 3 hodiny ujede první cyklista 3*24 km, to znamená, že se potkají ve 12 hodin 72 km od místa A.
4. V 6 hodin 15 minut vyjela z kasáren kolona aut jedoucí průměrnou rychlostí 32 km/h. V 7 hodin 18 minut vyjelo za kolonou terénní vozidlo. Jakou průměrnou rychlostí musí terénní vozidlo jet, má-li do vojenského výcvikového prostoru, vzdáleného od kasáren 72 km, dorazit současně s kolonou.
|
|
rychlost [v]
|
čas [t]
|
s = v . t
|
|---|---|---|---|
| 1. objekt A - kolona aut
|
32 km/h
|
t hod
|
72 km
|
| 2. objekt B - terénní vozidlo
|
v km/h
|
(t-1,05) hod
|
v(t-1,05) km
|
| celkem
|
|
|
72 km
|
Poznámka: Protože u kolony známe rychlost i vzdálenost, tak můžeme dopočítat čas. Terénní vozidlo vyjelo o 63 minut později, to je po převedení 1,05 hodiny (63:60).
$s_{1} = s_{2}$
$32t = 72$
$t = 2,25$
$72 = v(2,25-1,05)$
$1,2v = 72$
$v = 60$
Terénní vozidlo musí jet rychlostí 60 km/h.
5. Kamión jede po dálnici z Prahy do Bratislavy průměrnou rychlostí 72 km/h. V okamžiku, kdy je kamión od Prahy 54 km, vyjíždí z Prahy osobní auto, které jede rovněž do Bratislavy a jeho průměrná rychlost je 90 km/h. Kdy a na kterém kilometru dálnice Praha – Bratislava dohoní osobní auto kamión?
|
|
rychlost [v]
|
čas [t]
|
s = v . t
|
|---|---|---|---|
| 1. objekt A - kamión
|
72 km/h
|
t hod
|
72t km
|
| 2. objekt B - osobní auto
|
90 km/h
|
(t-0,75) hod
|
90(t-0,75) km
|
Poznámka: Musíme zjistit, za jak dlouho vyjelo osobní auto za kamiónem, tedy jak dlouho trvalo ujetí 54 km. t = s/v = 54/72 = 0,75
$s_{1} = s_{2}$
$72t = 90(t-0,75)$
$72t = 90t - 67,5$
$18t = 67,5$
$t = 3,75$
Osobní auto pojede 3 hodiny a ujede 270 km.
6. Z kasáren vyjela kolona aut průměrnou rychlostí 28 km/h do vojenského výcvikového prostoru a za 1 hodinu 15 minut vyjelo za kolonou terénní vozidlo rychlostí 63 km/h a přijelo do vojenského výcvikového prostoru současně s kolonou. Urči vzdálenost vojenského výcvikového prostoru od kasáren.
|
|
rychlost [v]
|
čas [t]
|
s = v . t
|
|---|---|---|---|
| 1. objekt A - kolona
|
28 km/h
|
t hod
|
28t km
|
| 2. objekt B - terénní vozidlo
|
63 km/h
|
(t-1,25) hod
|
63(t-1,25) km
|
$s_{1} = s_{2}$
$28t = 63(t-1,25)$
$28t = 63t - 78,75$
$35t = 78,75$
$t = 2,25$
$s = v . t$
$s = 28 . 2,25$
$s = 63$
Vzdálenost mezi kasárnami a vojenským prostorem je 63 km.
7. V 6 hodin 40 minut vyplul z přístavu parník rychlostí 12 km/h . Přesně v 10 hodin za ním vyplul motorový člun rychlostí 42 km/h. V kolik hodin dohoní člun parník?
|
|
rychlost [v]
|
čas [t]
|
s = v . t
|
|---|---|---|---|
| 1. objekt A - parník
|
12 km/h
|
t hod
|
12t km
|
| 2. objekt B - člun
|
42 km/h
|
(t-$3\frac{1}{3}$) hod
|
42(t-$3\frac{1}{3}$) km
|
$s_{1} = s_{2}$
$12t = 42(t-3\frac{1}{3})$
$12t =42(t-\frac{10}{3})$
$12t = 42t-140$
$30t =140$
$t = 4\frac{2}{3}$
Člun dohoní parník za 4 hodiny a 40 minut v 11 hodin 20 minut.
8. Oddíl připravuje celodenní výlet na Ještěd. Část cesty chce jet autobusem. Kdyby vyšel rychlostí 3 km/h, přišel by na autobusovou stanici 9 minut po odjezdu autobusu. Kdyby šel rychlostí 4 km/h, přišel by 6 minut před odjezdem autobusu. Urči vzdálenost autobusové stanice od tábora.
|
|
rychlost [v]
|
čas [t]
|
s = v . t
|
|---|---|---|---|
| 1. objekt A
|
3 km/h
|
(t + 0,15)hod
|
3(t + 0,15) km
|
| 2. objekt B
|
4 km/h
|
(t - 0,1) hod
|
4(t - 0,1) km
|
Poznámka: Při počítání s časem musíme převést minuty na desetinné číslo: 9/60 = 0,15 a 6/60 = 0,1
$s_{1} = s_{2}$
$3(t + 0,15) = 4(t - 0,1)$
$3t + 0,45 = 4t - 0,4$
$t = 0,85$
Zastávka je vzdálená 3 km [3 x (0,85 + 0,15)].
9. Mezi dvěma přístavišti jezdí parník. Cesta tam a zpět mu trvá 3 hodiny 45 minut. Po proudu pluje rychlostí 12 km/h , proti proudu rychlostí 8 km/h. Vypočítej vzdálenost mezi přístavišti.
|
|
rychlost [v]
|
dráha [s]
|
$t = \frac{s}{v}$
|
|---|---|---|---|
| 1. objekt A - po proudu
|
12 km/h
|
s km
|
$\frac{s}{12}$ hod
|
| 2. objekt B - proti proudu
|
8 km/h
|
s km
|
$\frac{s}{8}$ hod
|
|
|
|
|
3,75
|
$t = t_{1} + t_{2}$
$3,75 = \frac{s}{12} + \frac{s}{8} /*24$
$90 = 2s +3s$
$5s = 90$
$s = 18$
Mezi přístavišti je 18 km.
10. Cyklista jel z osady do města. První polovinu cesty, vedoucí převážně do kopce, jel rychlostí 10 km/h, druhou polovinu cesty, která převážně klesala, jel rychlostí 18 km/h. Celá cesta mu trvala 56 minut. Urči vzdálenost osady a města.
|
|
rychlost [v]
|
dráha [s]
|
$t = \frac{s}{v}$
|
|---|---|---|---|
| 1. objekt A - do kopce
|
10 km/h
|
s km
|
$\frac{s}{10}$ hod
|
| 2. objekt B - z kopce
|
18 km/h
|
s km
|
$\frac{s}{18}$ hod
|
|
|
|
|
$\frac{56}{60}$
|
Poznámka: $\frac{56}{60}=\frac{14}{15}$
$t = t_{1} + t_{2}$
$ \frac{14}{15} = \frac{s}{10} + \frac{s}{18} /*90$
$84 = 9s +5s$
$14s = 84$
$s = 6$
Polovina vzdálenosti mezi městem a osadou je 6 km, jejich celková vzdálenost je 12 km.
11. Auto ujelo vzdálenost mezi městy A a B za 4 hodiny. Kdyby se průměrná rychlost auta zvýšila o 17 km/h, ujelo by auto tuto vzdálenost o hodinu dříve. Urči rychlost auta a vzdálenost mezi městy A a B.
|
|
rychlost [v]
|
čas [t]
|
s = v . t
|
|---|---|---|---|
| 1. objekt A
|
(v + 17) km/h
|
3 hod
|
3(v + 17) km
|
| 2. objekt B
|
v km/h
|
4 hod
|
4v km
|
$s_{1} = s_{2}$
$3(v + 17) = 4v$
$3v + 51 = 4v$
$v = 51$
Rychlost auta je 51 km/h a vzdálenost mezi městy 204 km [4 * 51].
12. Rychlík dlouhý 85 m jede přes most rychlostí 72 km/h. Od okamžiku, kdy vjede lokomotiva na most, do okamžiku, kdy, kdy most opouští poslední vagón, uplyne 9 s. Jak dlouhý je most?
|
|
rychlost [v]
|
čas [t]
|
dráha [s]
|
|---|---|---|---|
| 1. objekt A - rychlík
|
72 km/h = 72 000 m/h
|
9 s = 0,15 min = 0,0025 h
|
s + 85 m
|
Poznámka: 9 s : 60 = 0,15 min; 0,15 : 60 = 0,0025 h
$s + 85 = 72000 . 0,0025$
$s = 180 - 85$
$s = 95 m$
Most je dlouhý 95 m.
13. Žáci z města M uskutečnili výlet do města N vzdáleného 74 km. Část cesty z M do N jeli vlakem průměrnou rychlostí 44 km/h a část cesty šli pěšky průměrnou rychlostí 4 km/h. Cesta vlakem byla o 30 minut kratší než pěší túra. Za jakou dobu se žáci dostali z města M do města N?
|
|
rychlost [v]
|
čas [t]
|
s = v . t
|
|---|---|---|---|
| 1. část cesty vlakem
|
44 km/h
|
(t - 0,5) hod
|
44(t - 0,5) km
|
| 2. část cesty pěšky
|
4 km/h
|
t hod
|
4t km
|
$s = s_{1} + s_{2}$
$74 = 44(t - 0,5) + 4t$
$74 = 44t - 22 +4t$
$48t = 96$
$t = 2$
První část cesty trvala 1,5 hodiny, druhá část cesty 2 hodiny, celá cesta trvala 3,5 hodiny.
14. Dvě letadla startující současně z letišť A a B letí navzájem proti sobě a setkají se za 20 minut. Vzdálenost letišť je 220 km a průměrná rychlost letadla letícího z letiště A je o 60 km/h větší než průměrná rychlost druhého letadla. Vypočítej průměrné rychlosti obou letadel.
|
|
rychlost [v]
|
čas [t]
|
s = v . t
|
|---|---|---|---|
| 1. objekt A
|
v km/h
|
$ \frac{1}{3} $ hod
|
$ \frac{v}{3} $ km
|
| 2. objekt B
|
(v + 60) km/h
|
$ \frac{1}{3} $ hod
|
$ \frac{v + 60}{3} $ km
|
| celkem
|
|
|
220 km
|
$s = s_{1}+ s_{2}$
$220 = \frac{v}{3} + \frac{v + 60}{3}$
$660 = v + v + 60$
$2v = 600 $
$v = 300$
Rychlost letadel je 300 a 360 km/h.
15. Dvě letadla letí z letišť A a B, vzdálených 420 km, navzájem proti sobě. Letadlo z letiště A odstartovalo o 15 minut později a letí průměrnou rychlostí o 40 km/h větší než letadlo z letiště B. Urči průměrné rychlosti obou letadel, jestliže se setkají 30 minut po startu letadla z letiště A.
|
|
rychlost [v]
|
čas [t]
|
s = v . t
|
|---|---|---|---|
| 1. objekt A
|
(v + 40)km/h
|
0,5 hod
|
0,5(v + 40) km
|
| 2. objekt B
|
v km/h
|
0,75 hod
|
0,75v km
|
| celkem
|
|
|
420 km
|
$s = s_{1}+ s_{2}$
$420 = 0,5(v + 40) + 0,75v$
$420 = 0,5v + 20 + 0,75v$
$1,25v = 400$
$v = 320$
Letadla letí rychlostmi 320 km/h a 360 km/h.
Obtížnější slovní úlohy na pohyb
16. Z Kutné Hory směrem ke Kolínu vyjel v 6 hodin 30 minut cyklista A průměrnou rychlostí 12 km/hod. V 7 hodin 40 minut vyjel z téhož místa opačným směrem na Čáslav cyklista B rychlostí 18 km/hod. V kolik hodin bude vzdálenost mezi cyklisty 79 km. Výsledek udejte v hodinách a minutách. Jak daleko od Kutné Hory bude v téže době cyklista B?
|
|
rychlost [v]
|
čas [t]
|
s = v . t
|
|---|---|---|---|
| 1. objekt A
|
12 km/h
|
t hod
|
12t km
|
| 2. objekt B
|
18 km/h
|
$t - \frac{7}{6}$ hod
|
$18(t - \frac{7}{6})$ km
|
| celkem
|
|
|
79 km
|
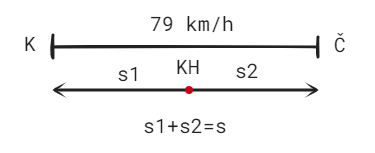
$s = s_{1}+ s_{2}$
$79 = 12t + 18(t - \frac{7}{6})$
$79 = 12t + 18t -21$
$30t=100$
$t = \frac{10}{3}=3h\;20\;min$
$3\; h\; 20\; minut\; +\; 6\; h\; 30\; min\; =\; 9\; h\; 50\; min$
Vzdálenost 79 km bude mezi cyklisty v 9 h 50 minut
Cyklista z Čáslavi jel 2 h 10 min a za tu dobu ujel 39 km.
17. Cesta kolem, přehrady je dlouhá 8 km. Z jednoho místa současně vyběhl běžec průměrnou rychlostí 12 km/hod. a opačným směrem vyjel cyklista. Určete průměrnou rychlost cyklisty, potká-li se s běžcem za 15 minut.
|
|
rychlost [v]
|
čas [t]
|
s = v . t
|
|---|---|---|---|
| 1. objekt A
|
12 km/h
|
0,25 hod
|
12 . 0,25 km
|
| 2. objekt B
|
v km/h
|
0,25 hod
|
0,25v km
|
| celkem
|
|
|
8 km
|
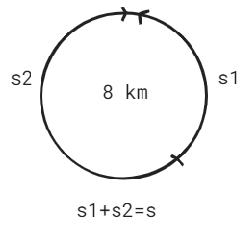
$s = s_{1}+ s_{2}$
$8 = 12 . 0,25 + 0,25v$
$0,25v = 5$
$v = 2\;km/h$
Průměrná rychlost cyklisty je 20 km/hod.
18. Jiráskovi jeli autem na dovolenou do Itálie. Po 10 minutách jízdy se na 20 minut zastavili na odpočívadle a opravovali auto. Jejich syn zjistil, že zapomněli vzít cestovní pasy a vydal se za nimi na motocyklu přesně za 30 minut po jejich odjezdu. Jakou průměrnou rychlostí musel jet, když je dohonil po ujetí 132 kilometrů a auto jelo průměrnou rychlostí 72 km/hod?
|
|
rychlost [v]
|
čas [t]
|
s = v . t
|
|---|---|---|---|
| 1. objekt A
|
72 km/h
|
$\frac{13}{6}$ hod
|
132 km
|
| 2. objekt B
|
v km/h
|
$\frac{5}{3}$ hod
|
132 km
|
| celkem
|
|
|
8 km
|
Jiráskovi

$\large \frac{1}{2}+\frac{5}{3}=\frac{13}{6}$
syn
$\large \frac{13}{6}-\frac{1}{2}=\frac{10}{6}=\frac{5}{3}$
$\large v=\frac{s}{t}=\frac{132}{\frac{5}{3}}=79,2\;km/h$
Syn jel rychlostí 79,2 km/h.
19. Nákladní auto vozí na stavbu písek. Jezdí-li průměrnou rychlostí 30 km/hod, trvá mu jedna cesta půl hodiny. Jakou rychlostí by muselo auto jezdit, aby zkrátilo každou jízdu o pět minut?
|
|
rychlost [v]
|
čas [t]
|
s = v . t
|
|---|---|---|---|
| 1.rychlost A
|
30 km/h
|
$\frac{1}{2}$ hod
|
15 km
|
| 2. rychlost B
|
v km/h
|
25 minut = $\frac{5}{12}$ hod
|
$v \times \frac{5}{12}$ km
|
$ s_{1}= s_{2}$
$15 =v \times \frac{5}{12}$
$180 =5v$
$v=36\;km/h$
Aby byla cesta o pět minut kratší, musí jet auto průměrnou rychlostí 36 km/h.
20. Turista šel 1/3 cesty rychlostí 4,5 km/hod, 0,4 cesty rychlostí 4 km/hod a zbývající 4 km rychlostí 5 km/hod. Kolik kilometrů ušel a jak dlouho mu trvala cesta? Čas počítejte ve zlomcích hodiny.
|
|
s [km]
|
|---|---|
| první část cesty | $\frac{1}{3}x$
|
| druhá část cesty | $\frac{2}{5}x$
|
| třetí část cesty | 4 km
|
| celkem | $x=\frac{1}{3}x+\frac{2}{5}x+4$
|
$x=\frac{1}{3}x+\frac{2}{5}x+4$
$15x=5x+6x+60$
$4x=60$
$x=15\;km$
|
|
dráha [s]
|
rychlost [v]
|
čas[t]=s/v |
|---|---|---|---|
| první část cesty | 5 km | 4,5 km/h | 5:4,5=50/45 h |
| druhá část cesty | 6 km | 4 km/h | 6:4 h |
| třetí část cesty | 4 km
|
5 km h | 4:5 h |
| celkem | 15 km |
|
|
$\frac{50}{45}+\frac{3}{2}+\frac{4}{5}=\frac{100+135+72}{90}=\frac{307}{90}=3\frac{37}{90}\;h$
Cesta trvala $3\; \frac{37}{90}\;h$
21. Z křižovatky dvou navzájem kolmých silnic odjíždí ve stejném okamžiku osobní automobil průměrnou rychlostí 96 km/hod a nákladní auto průměrnou rychlostí 72 km/hod. Každé auto jede po jiné silnici. Určete přímou vzdálenost aut po 5 minutách jízdy.
5 minut je jedna dvanáctina hodiny.
|
|
rychlost [v]
|
čas [t]
|
s = v . t
|
|---|---|---|---|
| 1.objekt A
|
96 km/h
|
$\frac{1}{12}$ hod
|
8 km
|
| 2. objekt B
|
72 km/h
|
$\frac{1}{12}$ hod
|
6 km
|

$c^{2}\;=\; a^{2}\;+\;b^{2}$
$c^{2}\;=\; 8^{2}\;+\;6^{2}$
$c^{2}\;=\; 64\;+\;36$
$c^{2}\;=\;100$
$c\;=\;\sqrt{100}$
$c\;=\;10\;km$
Přímá vzdálenost po 5 minutách jízdy bude 10 km.