Obsah nám říká, jak velkou plochu daný útvar zaujímá. Třeba jak velký máme byt nebo pozemek – kolik metrů čtverečních ($m^2$), hektarů (ha), centimetrů čtverečných ($cm^2$) atd.
Základní jednotkou obsahu je metr čtverečný → $m^2$
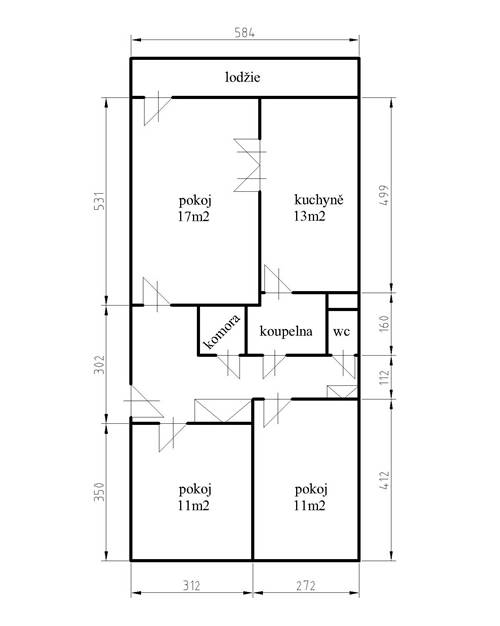
Představte si, že byste měli spočítat plochu bytu na obrázku. Z obrázku vyplývá, že byt má rozměry 584 cm a 1183 cm a jeho plocha je obdélníková. Obsah obdélníku vypočítáme tak, že šířku násobíme délkou.
$S=a.b$
$S=584.1183$
$S=690872\;cm^2\;=\;69\;m^2$
Plocha bytu (obsah obdélníku) je tedy 69 metrů čtverečních.

Čára, která vede po obvodu rovinného útvaru se nazývá obvod.
Obvodem může být například plot kolem pozemku, stužka potřebná pro ovázání, stopa, kterou zanechá pneumatika na zemi, manžeta na pračce, čára na hřišti apod..
Základní vzorce pro výpočet obsahu a obvodu
Obvod trojúhelníku $O = a + b + c$
Obsah trojúhelníku $S = \frac{a\times v_a}{2}$
Obvod čtverce $O = 4\times a$
Obsah čtverce $S = a^2$
Obvod obdélníku $O = 2(a + b)$
Obsah obdélníku $S = a \times b$
Obvod kruhu $O = 2\pi r$
Obsah kruhu $S = \pi r^2$
Obvod kosočtverce $O = 4\times a$
Obsah kosočtverce $S = a \times v_a$ $S = \frac{u_1 \times u_2}{2}$
Obvod kosodélníku $O = 2(a + b)$
Obsah kosodélníku $S = a\times v_a$
Obvod lichoběžníku $O = a + b + c + d$
Obsah lichoběžníku $S = \frac{(a + c)\times v}{2}$
Základní vzorce pro výpočet povrchu, objemu
Povrch nám říká například kolik tapety potřebujeme k polepení daného tělesa, jedná se o povrch vnější části tělesa. Základní jednotkou jsou metry čtverečné ($m^2$).
Objem nám pak říká, kolik například vody se do daného tělesa vejde, jedná se o vnitřek tělesa. Základní jednotkou jsou metry krychlové ($m^3$). Velmi často se objem udává v litrech.
Napíšeme si převod mezi litry a metry krychlovými:
$1m^3 = 1000 l$
$1 l = \frac{1}{1000} m^3 = 0,001 m^3$
Povrch budeme značit písmenem S a objem písmenem V.
Objem krychle $V = a^3$
Povrch krychle $S = 6\times a^2$
Objem kvádru $V = a\times b \times c$
Povrch krádru $S = 2(ab + bc + ac)$
Objem válce $V = \pi r^2v$
Povrch válce $S = 2\pi r(r+v)$
Objem pravidelného čtyřbokého jehlanu $V = \frac {a^2\times v}{3}$
Povrch pravidelného čtyřbokého jehlanu $S = a^2 + 2av_s$

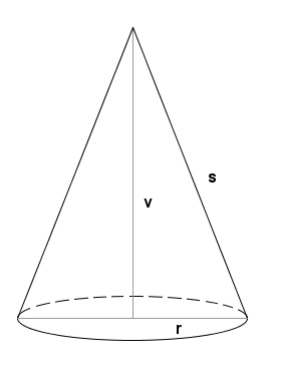
Objem kužele $V = \frac {\pi r^2v}{3}$
Povrch kužele $S = \pi r \times(r + \sqrt{r^2 v^2})$