Společný násobek a dělitel

Určete nejmenší společný násobek a největší společný dělitel čísel:


Příklad 1

$\large D(60, 90)$

$\large n(60, 90)$


1. Provedeme rozklad zadaných čísel na prvočísla.
$\Huge 60$





$\Huge 90$


$\large \swarrow$
$\large\searrow$


$\large \swarrow$
$\large\searrow$

$\huge 2$
$\times$
$\huge 30$



$\huge 2$
$\times$
$\huge 45$


$\large \swarrow$
$\large\searrow$


$\large \swarrow$

$\large\searrow$

$\huge 2$
$\times$
$\huge 15$



$\huge 3$
$\times$
$\huge 15$


$\large \swarrow$
$\large\searrow$


$\large \swarrow$
$\large\searrow$


$\huge 3$
$\times$
$\huge 5$


$\huge 3$
$\times$
$\huge 5$


2. Vypíšeme prvočísla z rozkladů. Prvočísla jsou ta čísla, která již nemají žádného dalšího dělitele (jsou na konci "ocásků").


$\large 60=2 \times 2 \times 3 \times 5$
$\large 90=2 \times 3 \times 3 \times 5$


3. Určíme největšího dělitele tak, že vypíšeme prvočísla, která tvoří dvojice.

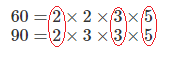
$\large D(60, 90)=2\times 3 \times 5= 30$


4. Určíme nejmenší násobek tak, že postupně vypíšeme nejvyšší počet jednotlivých prvočísel z obou rozkladů.


$\large n(60, 90)=2\times 2 \times 3 \times 3 \times 5= 180$


Pozn: V rozkladech jsou dvojky, trojky a pětky. Číslo 2 je nejvíce 2x, číslo 3 je také 2x a číslo 5 1x.


Příklad 2

$\large D(36, 48)$

$\large n(36, 48)$
$\Huge 36$





$\Huge 48$



$\large \swarrow$
$\large\searrow$


$\large \swarrow$
$\large\searrow$


$\huge 2$
$\times$
$\huge 18$



$\huge 2$
$\times$
$\huge 24$



$\large\swarrow$
$\large\searrow$


$\large\swarrow$

$\large\searrow$


$\huge 2$
$\times$
$\huge 9$



$\huge 2$
$\times$
$\huge 12$



$\large \swarrow$
$\large\searrow$


$\large\swarrow$
$\large\searrow$


$\huge 3$
$\times$
$\huge 3$


$\huge 2$
$\times$
$\huge 6$









$\large\swarrow$
$\large\searrow$









$\huge 2$
$\times$
$\huge 3$




$\large 36=2 \times 2 \times 3 \times 3$
$\large 48=2 \times 2 \times 2 \times 2 \times 3$


$\large D(36, 48)=2\times 2\times 3= 12$

$\large n(36, 48)=2\times 2 \times 2 \times 2 \times 3 \times 3 = 144$


Příklad 3

$\large D(60, 75)$

$\large n(60, 75)$
$\Huge 60$





$\Huge 75$



$\large \swarrow$
$\large\searrow$


$\large \swarrow$
$\large\searrow$


$\huge 2$
$\times$
$\huge 30$



$\huge 3$
$\times$
$\huge 25$



$\large\swarrow$
$\large\searrow$


$\large\swarrow$

$\large\searrow$


$\huge 2$
$\times$
$\huge 15$



$\huge 5$
$\times$
$\huge 5$



$\large \swarrow$
$\large\searrow$








$\huge 3$
$\times$
$\huge 5$








$\large 60=2 \times 2 \times 3 \times 5$
$\large 75=3 \times 5 \times 5 $


$\large D(60, 75)=3\times 5= 15$

$\large n(60, 75)=2\times 2 \times 3 \times 5 \times 5  = 300$


Příklad 4

$\large D(35, 56)$

$\large n(35, 56)$
$\Huge 35$





$\Huge 56$



$\large \swarrow$
$\large\searrow$


$\large \swarrow$
$\large\searrow$


$\huge 5$
$\times$
$\huge 7$



$\huge 2$
$\times$
$\huge 28$









$\large \swarrow$

$\large\searrow$








$\huge 2$
$\times$
$\huge 14$









$\large\swarrow$
$\large\searrow$








$\huge 2$
$\times$
$\huge 7$



$\large 35=5 \times 7$
$\large 56=2 \times 2 \times 2 \times 7$


$\large D(35, 56)=7$

$\large n(35, 56)=2\times 2 \times 2 \times 5 \times 7 = 280$


Příklad 5

$\large D(120, 135)$

$\large n(120, 135)$
$\Huge 120$





$\Huge 135$



$\large \swarrow$
$\large\searrow$


$\large\swarrow$
$\large\searrow$


$\huge 2$
$\times$
$\huge 60$



$\huge 3$
$\times$
$\huge 45$



$\large\swarrow$
$\large\searrow$


$\large\swarrow$

$\large\searrow$


$\huge 2$
$\times$
$\huge 30$



$\huge 3$
$\times$
$\huge 15$



$\large \swarrow$
$\large\searrow$


$\large\swarrow$
$\large\searrow$


$\huge 2$
$\times$
$\huge 15$


$\huge 3$
$\times$
$\huge 5$



$\large \swarrow$
$\large\searrow$








$\huge 3$
$\times$
$\huge 5$








$\large 120=2 \times 2 \times 2 \times 3 \times 5$
$\large 135=3 \times 3 \times 3 \times 5$


$\large D(120, 135)=3\times 5= 15$

$\large n(120, 135)=2\times 2 \times 2 \times 3 \times 3 \times 3 \times 5= 1080$